CS 144 Checkpoint 1 - Reassembler

“In this lab you’ll write the data structure that will be responsible for this reassembly: a Reassembler. It will receive substrings, consisting of a string of bytes, and the index of the first byte of that string within the larger stream. Each byte of the stream has its own unique index, starting from zero and counting upwards. As soon as the Reassembler knows the next byte of the stream, it will write it to the Writer side of a ByteStream — the same ByteStream you implemented in checkpoint 0. The Reassembler’s “customer” can read from the Reader side of the same ByteStream.”

In this checkpoint, we are tasked to implement a stream reassembler. We will receive data segments in random order through

void insert( uint64_t first_index, std::string data, bool is_last_substring );

and we need to assemble them into the correct order and send it down to our ByteStream as soon as the next byte is known. We also need to support querying for how many bytes are currently being processed through

uint64_t bytes_pending() const;

Internally, we need to maintain a buffer with a size of available_capacity.

Intervals

We are working with segments of bytes. So let’s define some terminology about “intervals” to make the discussion easier. An interval is a set \(I=[a,b) := \{x \in\mathbb{N}: a\leq x, x < b, a \leq b \in\mathbb N\}\). The interval \([a,a)=\emptyset\). Two intervals \(I_1=[a,b), I_2=[c,d)\) are disconnected if \(c > b\) or \(a > d\), which really means they cannot be unioned to make up a larger interval. Define the function, \(\text{start}([a,b))=a\), \(\text{end}([a,b))=b\), and \(\text{size}([a,b)) = b - a\). Here is a possible way to implement an interval in C++:

template<std::totally_ordered T>
struct Interval
{
  T start;
  T end;

  [[nodiscard]] constexpr T size() const 
  { 
    return end - start; 
  }

  [[nodiscard]] constexpr bool operator==( const Interval& other ) const 
  { 
    return this->start == other.start && this->end == other.end; 
  }

  [[nodiscard]] constexpr bool operator<( const Interval& other ) const
  {
    if ( this->start < other.start ) {
      return true;
    }
    if ( this->start > other.start ) {
      return false;
    }
    return this->end < other.end;
  }
};

We also defined an order on intervals: the values of start is compared first, if it ties, we compare end. This requires the type T of start and end to be ordered, C++ 20 concepts makes this restriction easy to express.

It is not hard to compute the intersection of two intervals.

template<std::totally_ordered T>
struct Interval
{
  // ...
  [[nodiscard]] static constexpr bool intersect( const Interval<T>& a, const Interval<T>& b )
  {
    return b.start < a.end && a.start < b.end;
  }

  [[nodiscard]] static constexpr std::optional<Interval<T>> intersection( const Interval<T>& a, const Interval<T>& b )
  {
    if ( !intersect( a, b ) ) {
      return std::nullopt;
    }
    return std::make_optional<Interval<T>>( std::max( a.start, b.start ), std::min( a.end, b.end ) );
  }
}

Our first observation is that we are essentially maintaining an interval \(B=[h, h + a)\) of bytes as a buffer where \(h\) is the first unassembled index and \(a\) is the available_capacity, the insert function will supply an interval \(D=[f, f + s)\) of bytes where \(f\) is the first_index and \(s\) is data.size(). Any bytes with index \( < h\) has already been pushed to the byte stream, and any bytes with index \(\geq h+a\) exceeds the capacity of the byte stream, so they can be safely ignored. The data we need to process have indexes within the intersection between \(I\) and \(J\). Now, we only need to maintain a collection of disconnected intervals \(K_i\). We push an interval \(K\) into the byte stream whenever \(\text{start}(K) =h\), then remove it from the collection, we will refer to the interval \(K\) as the “minimum” interval from now on. Notice that the “minimum” interval is unique, at most one interval can contain the first unassembled byte since all intervals are disconnected. Querying for the remaining bytes is equivalent of computing \(\sum_i \text{size}(K_i)\). The insertion is trickier, we need to somehow maintain the disconnected invariant efficiently. The problem now becomes “what’s the best data structure that supports insertion, summation, finding minimum and removing minimum on disconnected intervals”?

Bitmap

One possible approach is to maintain a bitmap vector<bool> used_, where used_[i] is true if and only if the byte at index i is currently inside our buffer. Let’s analyse the performance for each of the operation we need to do:

• Inserting an interval of length \(L\) requires filling used_[start] to used_[end - 1] with true. This has linear time complexity \(O(L)\).
• Summation requires counting the number of true in the used_ bitmap. This has linear time complexity with respect to the number of bytes inside the buffer.
• Finding the minimum involves a linear scan starting from used_[0] to the first index i where used_[i] is false.
• Removing the minimum requires filling the minimal interval with false, which is again linear with respect to the number of bytes we need to process.

Bitmap is not attractive in terms of time complexity. We are representing intervals in a very inefficient way, which leads us to store and update a lot of unnecessary information. It does have the advantage of zero allocation, and possibly good cache locality. But the fact that the time complexity is proportional to the number of bytes makes it too asymptotically slow for the job.

Binary Search Tree

Using a tree-like data structure for storing intervals might bring down the time complexity. Indeed, it is possible to use a std::set<Interval<uint64_t>> for storing intervals with respect to the order we defined previously. It is difficult to enforce all intervals in the BST to be disconnected from one another. However, this isn’t really a problem, we can simply delay merging overlapping intervals to the point when we compute the minimum.

Remember, an interval is just a pair of start and end indexes, so we need to store the actual bytes in a separate std::vector<char> buffer and reference them using indexes when needed. This makes interval operations (merging, slicing, etc…) cheap because we are operating on pairs of uint64_t instead of copying chunks of bytes. Let’s analysis the time complexity again.

• Insertion. We insert \(I \cap J\) as is into the BST, this takes \(O(\log n)\) where \(n\) is the number of intervals in the BST.
• Summation. We have to compute the disjoint intervals. It takes \(O(n)\) to obtain a sorted list of intervals by doing an in order traversal, and \(O(n)\) to merge connected intervals and compute the sum, where \(n\) is again the number of intervals in the BST.
• Finding and removing the minimum. It takes \(O(\log n)\) to find the smallest interval inside the tree, we can also remove it in \(O(\log n)\) time. But we are not done yet, the next smallest interval might connect to the first one, so it should be removed and merged with the first interval if needed. In the worst case, all intervals are connected and we have one giant connected interval, it takes \(O(n \log n)\)¹ time to merge them all.

A BST has great time complexity for the problem. Importantly, its time complexity grows with respect to the number of intervals we need to process, the length of each interval does not matter here, which makes it way better than a bitmap. However, in practice, std::set involves a lot of small allocations, fragmented memory and a large constant factor for maintaining the balanced tree structure. It turns out we can get a much better constant factor if we are willing to give in a bit on the asymptotic time complexity of the summation operation. In fact, the throughput benchmark does not call bytes_pending anyway, so it is a trade off I am willing to make.

Heap

A heap is a complete binary tree that allows us to access the smallest (or the largest) element in \(O(1)\) time. We can use a std::priority_queue to act as a min heap for storing our data. It can be implemented on a std::vector which makes it much more cache friendly than a std::set. Insertion and processing the minimum are similar to the BST implementation. For the summation operation, it takes \(O(n \log n)\) to obtain a sorted list from heap instead of \(O(n)\) for the BST. In fact, we can simply sort on the std::vector and the min heap’s invariants will be kept. This is the data structure I picked in the end.

Storing bytes

We have discussed a lot about how to store and process the index intervals. Now let’s talk about how to store the bytes. Of course, there are many ways to approach this. The naive approach is to allocate a std::vector<char> that has the same capacity as the underlying byte stream. The byte head_index_ points to is stored at the start of the vector. After a push to the underlying byte stream, we update the head_index_ and move the rest of the data forward. This involves a lot of unnecessary copying. We can then improve it by applying the same technique we used in checkpoint 0 to create a “sliding vector” that reduces unnecessary copying.

But there is another cleverer way to approach this: what about sharing the same buffer between the reassembler and the byte stream? The byte stream is responsible for the data from the first unpopped index to the first unassembled index, and the reassembler is responsible for the data from the first unassembled index to the first unacceptable index. These two ranges are disjoint from one another, and their total size equals to the capacity of the byte stream.

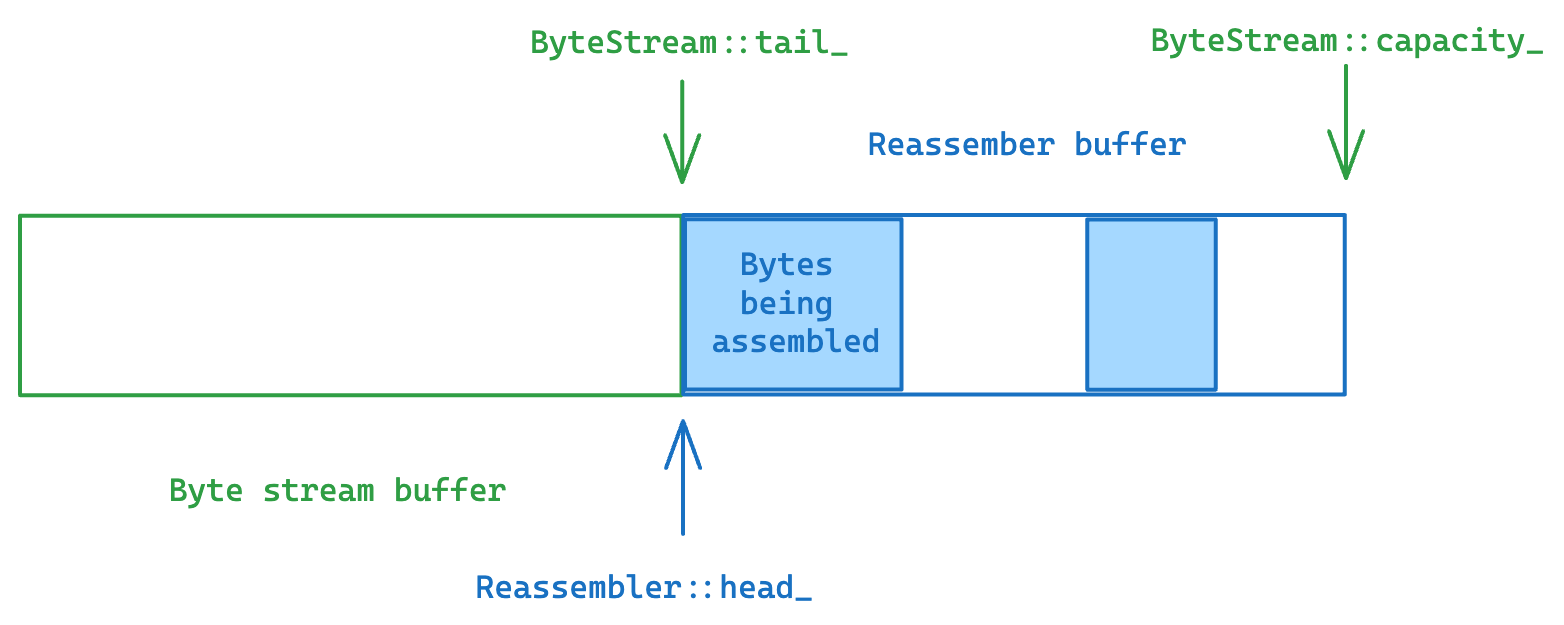
In this case, the Writer::push can be a simple update on pointers without involving any extra copying.

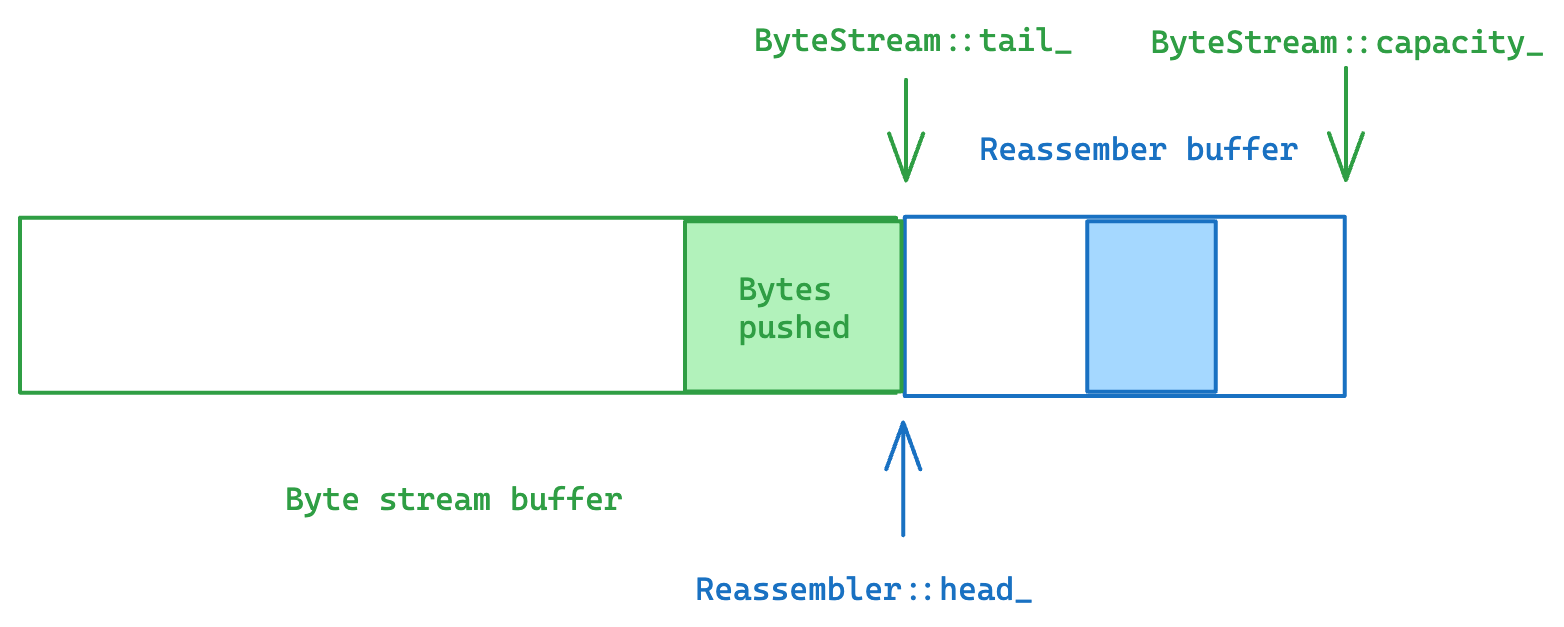
Every time the reassembler received a new piece of data, we ask the byte stream to return a std::span of its available buffer

std::span<char> Writer::available_buffer()
{
  return { std::begin( buffer_ ) + tail_, available_capacity() };
}

When the reassembler is ready to push some bytes to the byte stream, we can simply tell the byte stream to shift its tail and accept the new bytes who are constructed in place.

void Writer::emplace( uint64_t size )
{
  tail_ += size;
  bytes_pushed_ += size;
  size_ += size;
}

Profiling

My final implementation reached around 17 Gbit/s throughput on my machine.

pcloud@ubuntu:~/minnow$ cmake --build build --target check1
Test project /home/pcloud/minnow/build
      Start  1: compile with bug-checkers
 1/17 Test  #1: compile with bug-checkers ........   Passed    2.15 sec
      Start  3: byte_stream_basics
 2/17 Test  #3: byte_stream_basics ...............   Passed    0.01 sec
      Start  4: byte_stream_capacity
 3/17 Test  #4: byte_stream_capacity .............   Passed    0.01 sec
      Start  5: byte_stream_one_write
 4/17 Test  #5: byte_stream_one_write ............   Passed    0.01 sec
      Start  6: byte_stream_two_writes
 5/17 Test  #6: byte_stream_two_writes ...........   Passed    0.01 sec
      Start  7: byte_stream_many_writes
 6/17 Test  #7: byte_stream_many_writes ..........   Passed    1.87 sec
      Start  8: byte_stream_stress_test
 7/17 Test  #8: byte_stream_stress_test ..........   Passed    0.36 sec
      Start  9: reassembler_single
 8/17 Test  #9: reassembler_single ...............   Passed    0.01 sec
      Start 10: reassembler_cap
 9/17 Test #10: reassembler_cap ..................   Passed    0.01 sec
      Start 11: reassembler_seq
10/17 Test #11: reassembler_seq ..................   Passed    0.03 sec
      Start 12: reassembler_dup
11/17 Test #12: reassembler_dup ..................   Passed    0.92 sec
      Start 13: reassembler_holes
12/17 Test #13: reassembler_holes ................   Passed    0.01 sec
      Start 14: reassembler_overlapping
13/17 Test #14: reassembler_overlapping ..........   Passed    0.01 sec
      Start 15: reassembler_win
14/17 Test #15: reassembler_win ..................   Passed    3.72 sec
      Start 37: compile with optimization
15/17 Test #37: compile with optimization ........   Passed    1.31 sec
      Start 38: byte_stream_speed_test
             ByteStream throughput: 33.28 Gbit/s
16/17 Test #38: byte_stream_speed_test ...........   Passed    0.07 sec
      Start 39: reassembler_speed_test
             Reassembler throughput: 17.43 Gbit/s
17/17 Test #39: reassembler_speed_test ...........   Passed    0.12 sec

100% tests passed, 0 tests failed out of 17

Total Test time (real) =  10.60 sec
Built target check1

Note that all the benchmarks results shown are just for entertainment. They are not comparable across different machines. The same piece of code has completely different performance on a GitHub Action Runner.

text

ByteStream with capacity=32768, write_size=1500, read_size=128 reached 23.50 Gbit/s.
Test time =   0.06 sec
----------------------------------------------------------
Reassembler to ByteStream with capacity=1500 reached 24.70 Gbit/s.
Test time =   0.13 sec

Here is the critical section of the benchmark code

while ( not split_data.empty() ) {
  auto& next = split_data.front();
  reassembler.insert( get<uint64_t>( next ), move( get<string>( next ) ), get<bool>( next ) );
  split_data.pop();

  while ( reassembler.reader().bytes_buffered() ) {
    output_data += reassembler.reader().peek();
    reassembler.reader().pop( output_data.size() - reassembler.reader().bytes_popped() );
  }
}

output_data += reassembler.reader().peek() takes up half of the time, and the code we control is responsible for the other half.

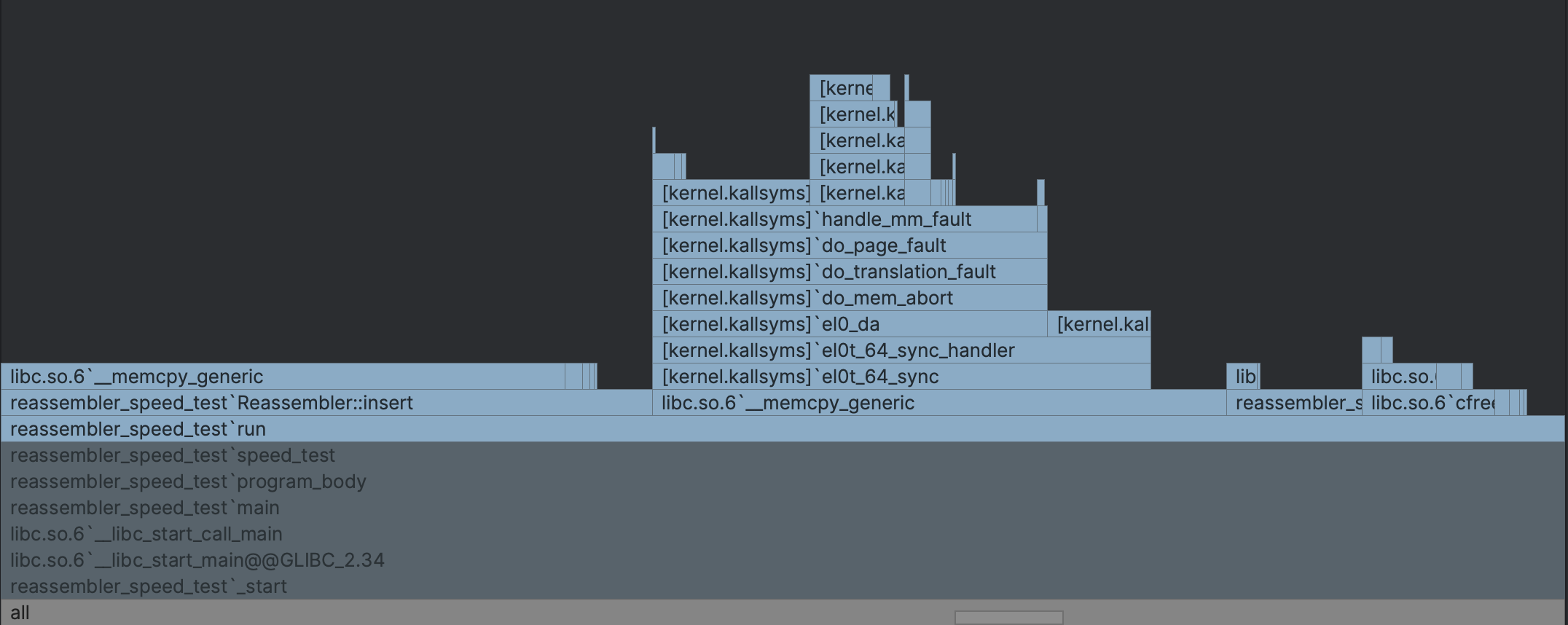
Upon a closer look, Reassembler::insert takes about 40% of the total time and Reader::pop takes about 10%.

Inside Reader::pop, we are doing memcpy 20% of the time. This is moving the “sliding queue” back to the front inside the byte stream as we discussed in checkpoint 0, and there isn’t much we can do about it.

Inside Reassembler::insert, we spent 85% of our time copying the data we were given into the buffer. It shows our selection of data structure is performant in this case. But why did we spend so much time on copying? One possible reason might be because we do not de-duplicate intervals when we copy them. We always copy the entire interval regardless whether part of it might already be in the buffer (supplied by a previous piece of data). Is that the problem? Unfortunately, the data used for the benchmarking is mostly non-overlapping. So the time we spent on copying is unavoidable.

But why is the throughput halved compared to the byte stream benchmark, if we are not doing much extra work? It’s mostly because the structure and parameters of the two benchmarks are vastly different, so their results can not be directly compared. The capacity of the byte stream is set to 1500 in the reassemble benchmark instead of 32768 in the byte stream benchmark, for example. The spec states

A top-of-the-line Reassembler will achieve 10 Gbit/s.

so it’s either our implementation is 70% topper-of-the-line, or my computer is 70% faster, or a combination of both. I am satisfied with the result.

This concludes Checkpoint 1.